三 平方 の 定理 表 228149

この表から2次合同方程式x 2 ≡a (mod 7)の解が存在するときのa、解が存在しないときのaが判明する。x 2 の列に登場する数は、ある整数xの平方をmod pの世界で考えた値である。つまり、a=1,4,2のときにx=1,2,3という解があることがわかる。2平方定理この定理はフェルマーの2平方定理とも呼ばれることがあり，証明はオイラーによってはじめてなされたとされています．定理．奇素数(奇数かつ素数，すなわち 3 以上の素数) \(p\) が 4 で割ると 1 余るとき，\(p\) は 2三角形の三辺の値を入力するだけだで簡単に角度がわかり助かりました。 2 1552 男 / 歳代 / エンジニア / 非常に役に立った / 使用目的

3d Cadで設計の総仕上げ 動きや質感まで確認してみよう そして 次のdiyへ ステイホームでdiyを極める 玄人志向なモノづくり 4 4 4 ページ Monoist

三 平方 の 定理 表

三 平方 の 定理 表-トップ 100 三 平方 の 定理 表 三平方の定理の利用 Ict教材eboard イーボード 特別な三角形 例題と練習 特別な三角形2 例題と練習 二等辺三角形の面積 例題と練習 三辺から三角形の面積を求める 三角定規型 暗記しておくべき直角三角形があります それはを参考にして，三平方の定理の証明を構想すると いった概略を示した簡易なものであった． その結果，授業をお願いした先生方からは，「三 平方の定理の証明を生徒が考えるのは困難ではな いか」，「三平方の定理と証明の両方を生徒に発見さ

中３数学 図でよくわかる三平方の定理 ピタゴラスの定理 の証明と計算問題 Irohabook

U adcは直角三角形であるから，acの長さがわかればadの長さが求められる。そこで，ま ず，u abcに注目し，三平方の定理を利用して，acの長さを求める。 u abcで三平方の定理より ac 5 5 10 5 cm ＝－＝（）`j 2 2 ←ac ab bc＝－22 さらに，u adcで三平方の定理より ad 4 5 41＝＋＝22 （cm）←ad dc ac＝＋22今回は『三平方の定理』という単元を 基礎から解説していきます。 三平方の定理は、いつ習う？ 学校によって多少の違いはありますが 大体は3年生の3学期に学習します。 中3の終盤に学習するにも関わらず 入試にはバンバンと出題されてきます。「三個の平方数の和」で表される数に関する定理のこと このページは 曖昧さ回避のためのページ です。 一つの語句が複数の意味・職能を有する場合の水先案内のために、異なる用法を一覧にしてあります。

特集 生徒が喜ぶ「三平方の定理」の授業 提言・「三平方の定理」は面白い教材 この教材を有効に生かすために ･･････ 上垣 渉;33 四平方和定理 本文的主要目的是證明拉格朗日定理：每一個正整數皆可表為四個整數的平方和及高斯 的三角形數定理：每一個正整數皆可表為三個三角形數的和。 331 尤拉恆等式 我們很容易證得如下的斐波那契恆等式： 2 22 y 1が成り立ちます。これで、三平方の定理を証明することができました！「平方」とは 2乗のことなので、「三平方の定理」と言われるゆえんは、直角三角形の「三」つの辺それぞれの「平方」、つまり a 2, b 2, c 2 の間に成り立つ関係式ということですね。

三平方の定理は、別名「ピタゴラスの定理」とも言います。 例えば、直角をはさむ2つの辺の長さが \(3cm\) と \(4cm\) の直角三角形の斜辺の長さを実際に測ってみると、\(5cm\) であることが分かります。三平方の定理とは 三平方の定理(基本問題1) 例題と練習 三平方の定理(基本問題2) 例題と練習 三平方の定理(四角形の対角線) 例題と練習 特別な三角形 例題と練習 特別な三角形2 例題と練習 二等辺三角形の面積 例題と練習 三辺から三角形の面積を求める平方数（へいほうすう）というのは、自然数の二乗で表される整数のことです。 ここでは元の数が100までの平方数を一覧表にして紹介します。 この平方数にはある特徴があります。 1～50までの数と51～100までの数の下2桁を見てもらえるとわかると思いますが、1と51、2と52と見ていくと下2桁

三平方の定理から円周率を計算してみる Yamav1 02bのブログ

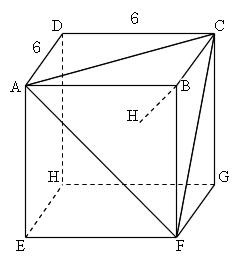
Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集

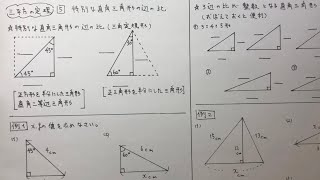
三平方の定理に当てはめて ac 2 =12 2 12 2 ac 2 =2 ac=±12 2 ac>0より ac=12 2 oからacに引いた垂線をomとすると これが四角錐の高さになる。 amはacの 1 2 なので am=6 2 ≫ o a c 15cm 15cm m 12 2 cm 6 2 cm oamで三平方の定理を使うと 15 2 =om 2 (6 2) 2 om 2 = om 2 =153 om=±3 17 om>0三平方の定理、立体の体積・表面積 解説 右図のような立体の体積・表面積は，四角錐の高さなどを三平方の定理で求めてから計算します。 右図は底面が1辺の長さ4cmの正方形，側面が1辺の長さ4cmの正三角形です。やまぐちっ子学習プリント教科書対応表（中学校3年数学） 01 式の展開と因数分解 02 平方根 ☆やまぐちっ子プラス 三平方の定理 17 ☆やまぐちっ子プラス 標本調査

三平方の定理とは 証明方法や例題についても解説 スタモ 受験 入試 学習の総合サイト

７章 三平方の定理 愛知県公立高校入試 数学 単元別過去問 問題プリントと解答 解説

を参考にして，三平方の定理の証明を構想すると いった概略を示した簡易なものであった． その結果，授業をお願いした先生方からは，「三 平方の定理の証明を生徒が考えるのは困難ではな いか」，「三平方の定理と証明の両方を生徒に発見さ三平方の定理は、別名「ピタゴラスの定理」とも言います。 例えば、直角をはさむ2つの辺の長さが \(3cm\) と \(4cm\) の直角三角形の斜辺の長さを実際に測ってみると、\(5cm\) であることが分かります。三平方の定理、立体の体積・表面積 解説 右図のような立体の体積・表面積は，四角錐の高さなどを三平方の定理で求めてから計算します。 右図は底面が1辺の長さ4cmの正方形，側面が1辺の長さ4cmの正三角形です。

わかりやすい三角比と基本公式 Irohabook

Mathematics 三平方の定理 ５ 空間図形と三平方の定理 働きアリ

数学史から入る「三平方の定理」 「三平方の定理」は，いつ，どのようにして発見されたか ･･････ 片野 善一郎三角関数は周期関数なので、逆関数は多価関数である。 逆関数の性質から以下が成り立つ： =,() = − / ≤ ≤ /ピタゴラスの定理 ピタゴラスの定理やオイラーの公式などから以下の基本的な関係が導ける 。 = ここで sin 2 θ は (sin(θ)) 2 を意味する。 この式を変形して、以下の式が導かれる：三平方の定理とは 三平方の定理(基本問題1) 例題と練習 三平方の定理(基本問題2) 例題と練習 三平方の定理(四角形の対角線) 例題と練習 特別な三角形 例題と練習 特別な三角形2 例題と練習 二等辺三角形の面積 例題と練習 三辺から三角形の面積を求める

年度用 中学校数学教科書内容解説資料 未来へひろがる数学

中３数学 図でよくわかる三平方の定理 ピタゴラスの定理 の証明と計算問題 Irohabook

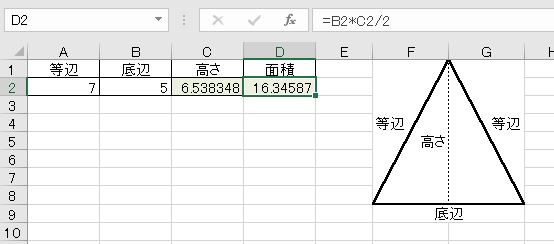
Sinθ cosθ tanθ の覚え方・弧度法・三角比の表まとめ」の記事も参考にしてみてください。 正弦定理 2つの視点から分かる公式の覚え方・考え方 三角形 \(ABC\) に対して、点 \(A,B,C\) の内角をそれぞれ角 \(A,B,C\) とおき 点 \(A\) の反三平方の定理は、別名「ピタゴラスの定理」とも言います。 例えば、直角をはさむ2つの辺の長さが \(3cm\) と \(4cm\) の直角三角形の斜辺の長さを実際に測ってみると、\(5cm\) であることが分かります。四平方和定理說明所有正整數均可表示為最多四個平方數的和。 特別的，三個平方數之和不能表示形如 4 k (8 m 7) 的數。 若且唯若 一個正整數可以表示 因數 中沒有形如 4 k 3 的素數的奇次方，則它可以表示成兩個平方數之和。

中3数学 三平方の定理5 特別な直角三角形の辺の比 すべて無料 星組の中学数学講座

中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット

数学 三平方の定理 中学数学に関する質問 勉強質問サイト

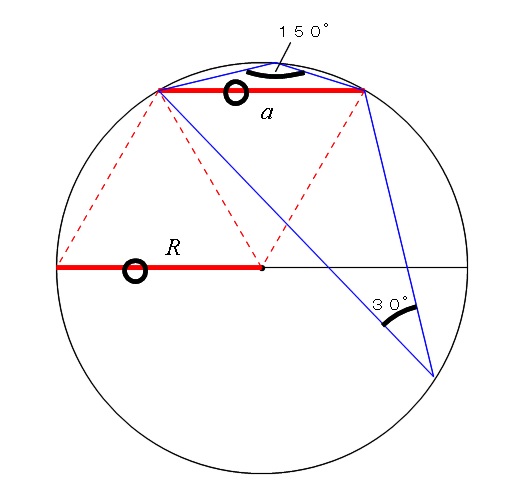
三角形の形状決定問題と三角比と辺で表された等式の証明

高校受験21 福岡県立高校入試 学力検査の出題範囲を一部除外 リセマム

なんで相対速度は引き算だと言っているのに ここでは三平方の定理を使うのですか Clear

三平方の定理 やややさしい数学

3d Cadで設計の総仕上げ 動きや質感まで確認してみよう そして 次のdiyへ ステイホームでdiyを極める 玄人志向なモノづくり 4 4 4 ページ Monoist

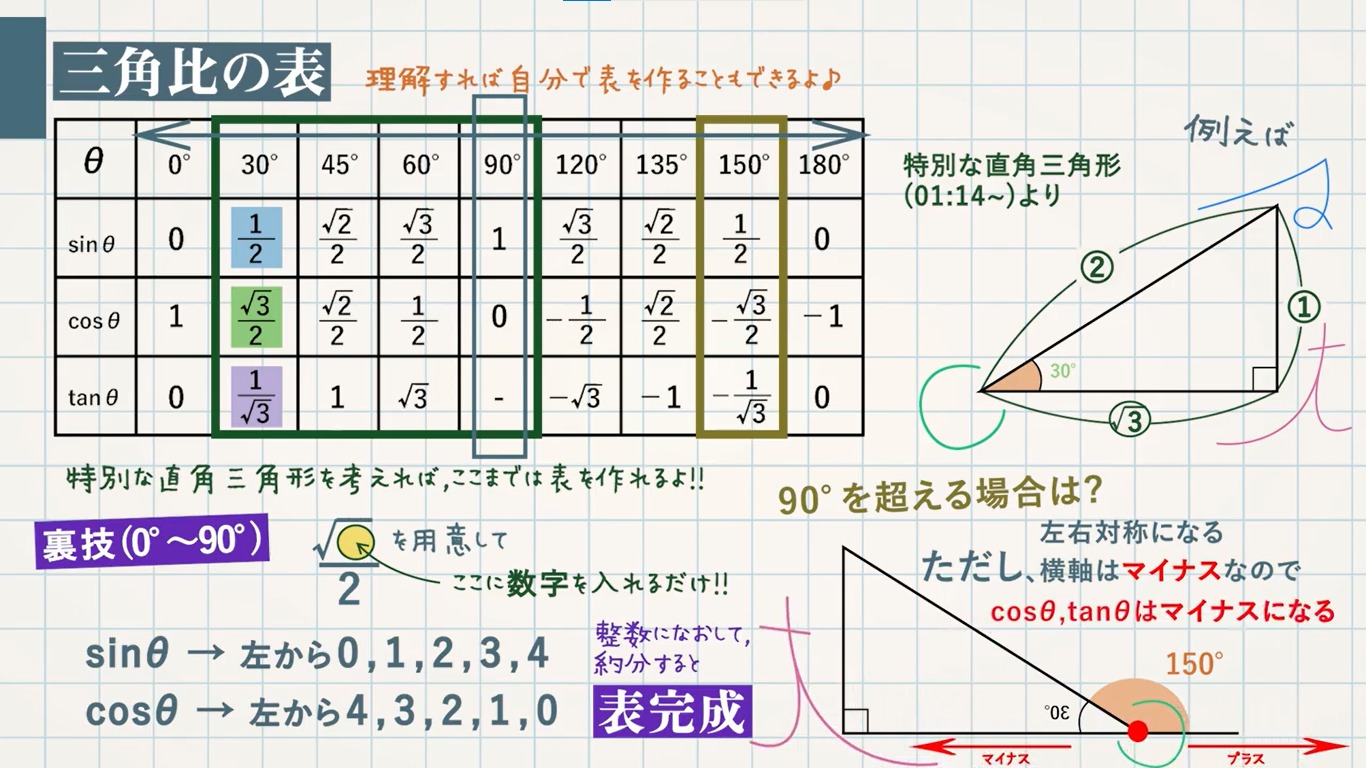
三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者

三平方の定理の証明 中学数学 By じょばんに マナペディア

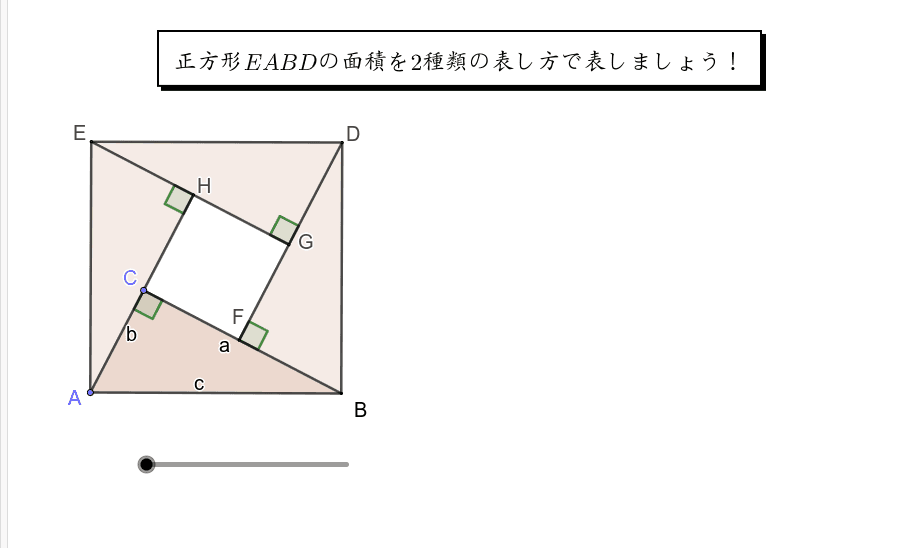
三平方の定理の証明 Geogebra

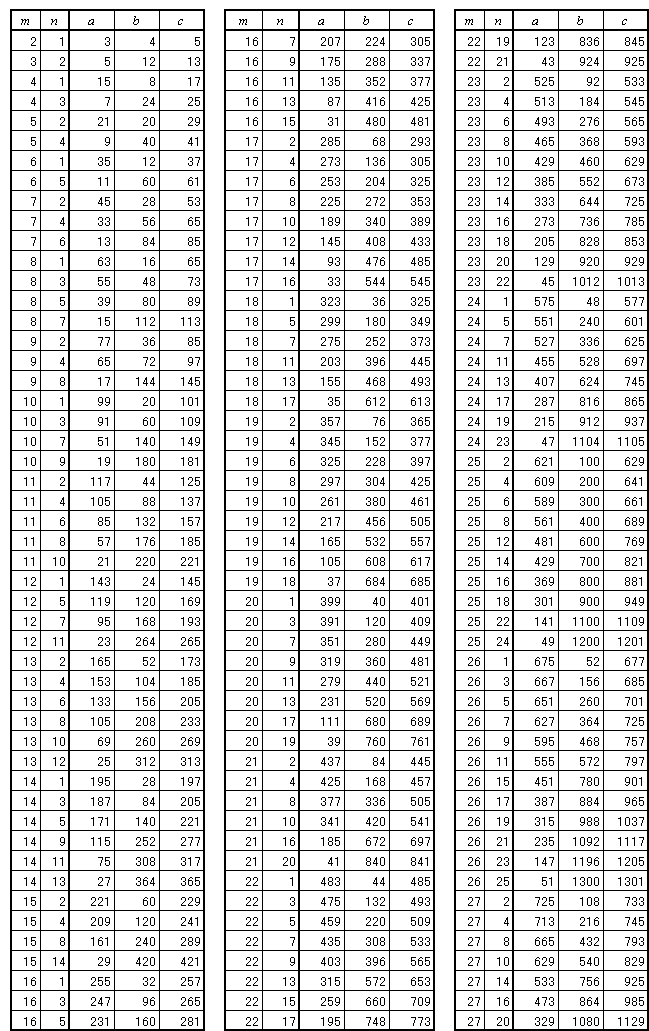
書評 ピタゴラスの定理

三角比を用いた計算問題をマスターしよう スタディクラブ情報局

神奈川県公立高校入試 出題範囲 あすもりのブログ

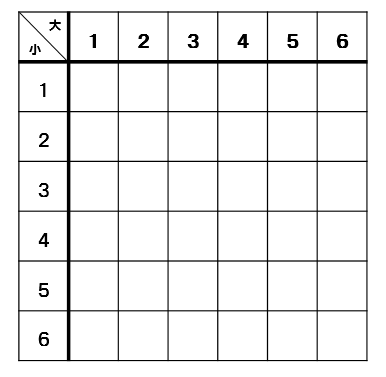
中学数学 さいころ2個の確率問題をパターン別に解説 数スタ

三角比の表の値 Sincostan の覚え方を解説 単位円でマイナスも定義 遊ぶ数学

中学３年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生

三角比 高校物理の備忘録

都立入試数学 三平方の定理を使わなくても解けるか 都立に入る

三平方の定理が一瞬で理解できる 公式 証明から計算問題まで解説 Studyplus スタディプラス

円と三平方の定理 中学数学に関する質問 勉強質問サイト

Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集

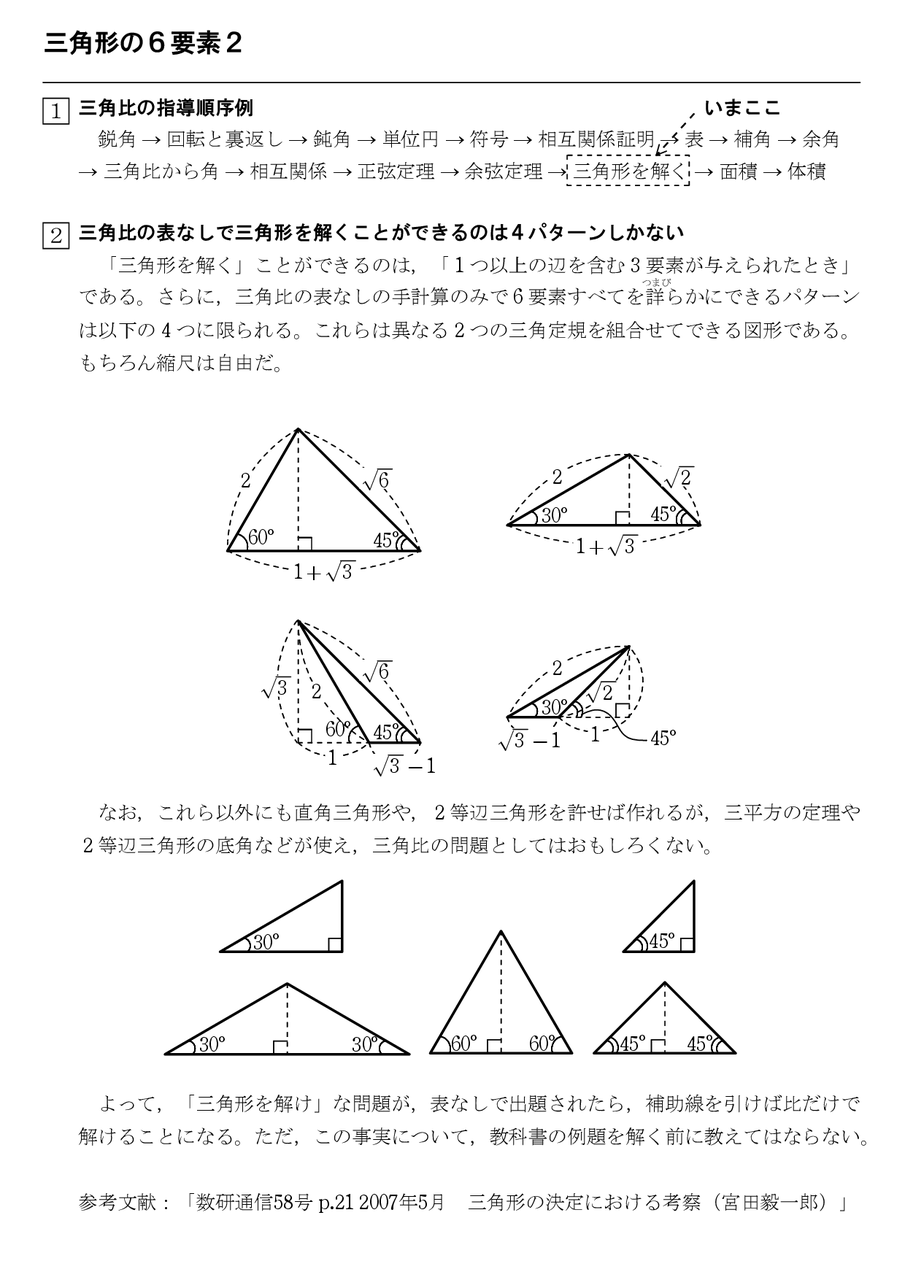
三角形の６要素２ 怜悧玲瓏 高校数学を天空から俯瞰する

三平方の定理が抜ける影響 とある個別の凡人講師

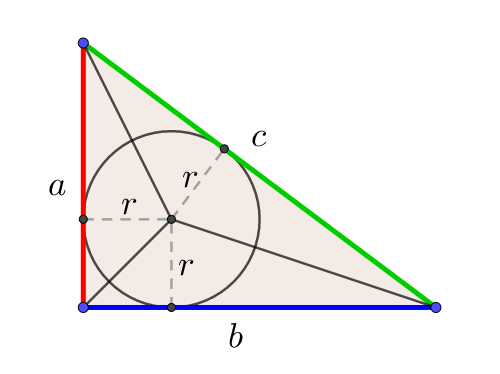
三平方の定理の証明４ 直角三角形と内接円 キソカラ

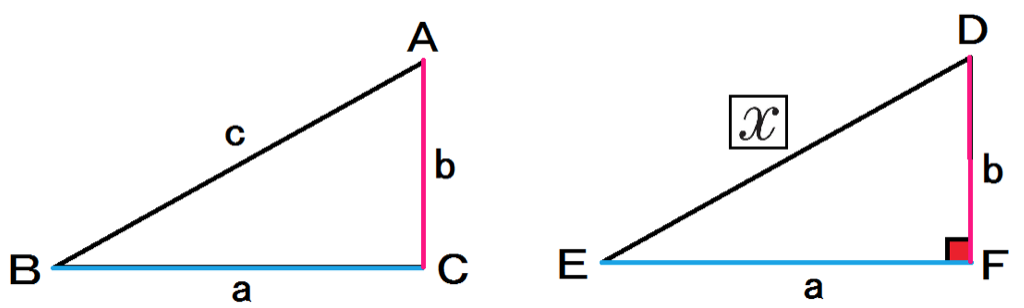
中3数学 2分でわかる 三平方の定理の逆 Qikeru 学びを楽しくわかりやすく

壁紙 押入れ トップ 100 三 平方 の 定理 表

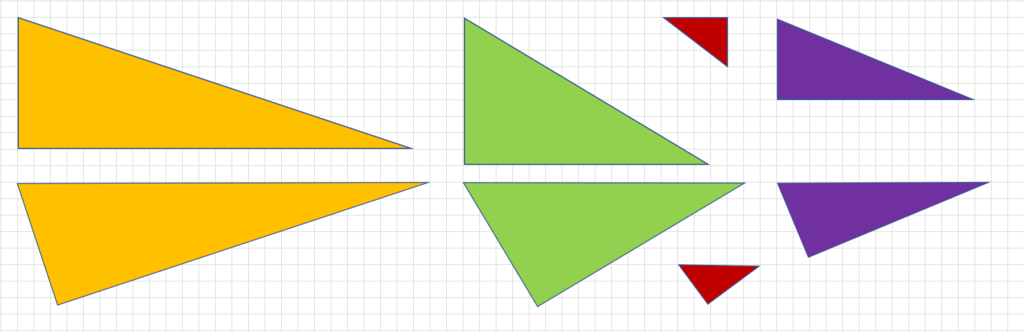
中学数学 直角三角形の三平方の定理とは ピタゴラス 平方根 の定理をexcelの図形で Curlpingの幸せblog

三平方の定理の利用 Ict教材eboard イーボード

壁紙 押入れ トップ 100 三 平方 の 定理 表

ট ইট র 小林克彦 都立高校入試で 三平方の定理が云々に対して とんちんかんなこと言ってる人 まあ落ち着けよと思う

Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集

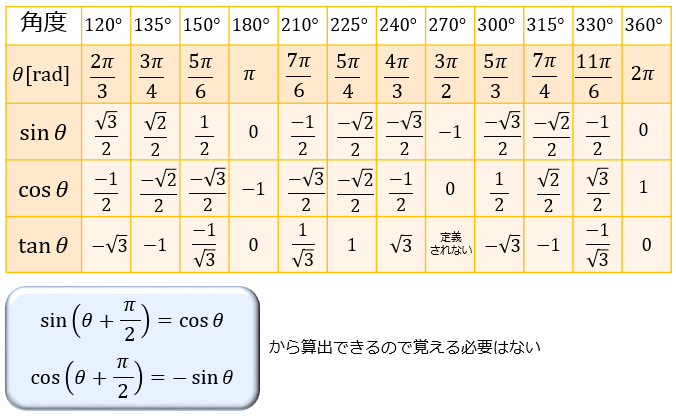
三角関数の基礎知識 Sin8 Cos8 Tan8 の覚え方 弧度法 三角比の表まとめ アタリマエ

都立高校入試対策 今年の受験生はこう戦え 上位高校 数学編 過去のブログ

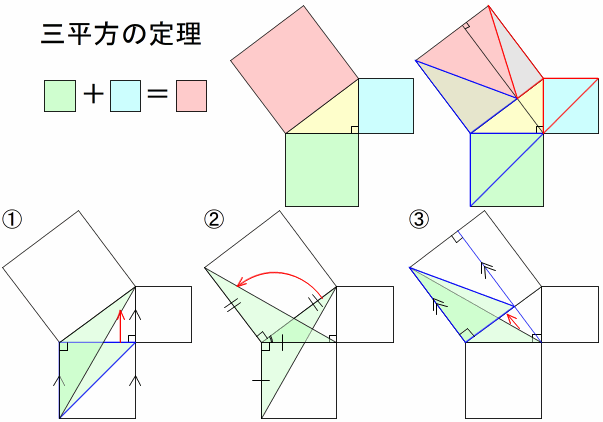
３ ４ ５の三角形で 本当に直角ができる Note Board

三角関数 Sin Cos Tanの表について 写真の表って全部覚える必要ありま 数学 教えて Goo

21年度 東京都立高校入試変更点とコメント 星火塾

高校数学 第2余弦定理 三平方の定理の一般化 と第1余弦定理の証明と利用 受験の月

証明にこだわる

必見 絶対知りたい三平方の定理の証明方法3選 見やすい図で即わかる 高校生向け受験応援メディア 受験のミカタ

高校受験で必須の証明を 中学数学で用いる定理と定義一覧表 で苦手克服 マニア目線で明瞭 解決

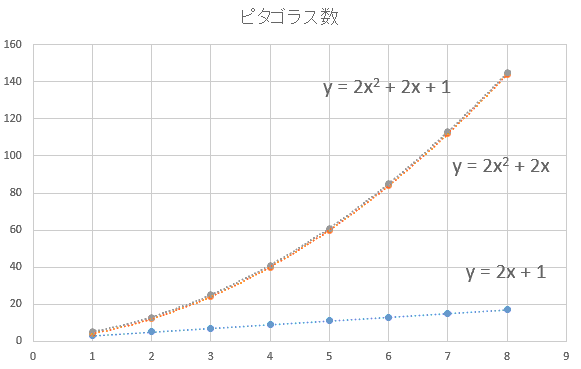
数の不思議 奇数の和でできるピタゴラス数 Note Board

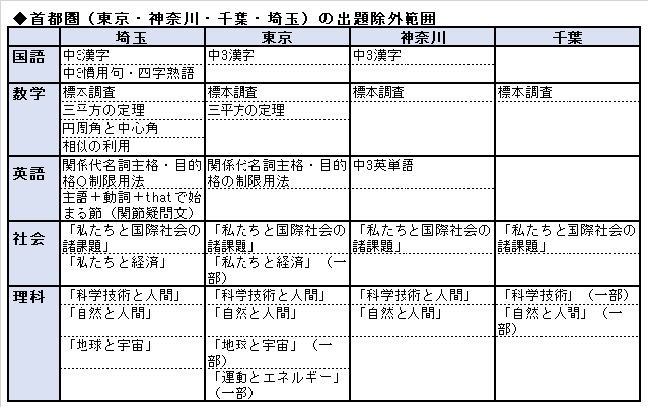
公立入試出題除外範囲 関東各都県の最終まとめ 梅野弘之オフィシャルブログ

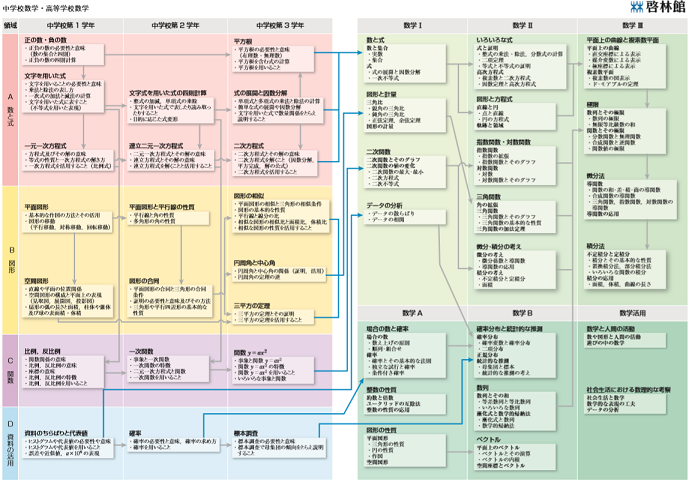
中学数学やり直しのおすすめの参考書は 高校生 社会人でも使えます 予備校なら武田塾 可児校

三平方の定理から円周率を計算してみる Yamav1 02bのブログ

三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ

三角比の表 について どうして75度と90度がないんですか 90 Yahoo 知恵袋

三角比の定義は １分でわかる定義 覚え方 表 直角三角形と単位円との関係

8 2三角比 三平方の定理 三角関数表 Youtube

三平方の定理の一般解 理系ノート

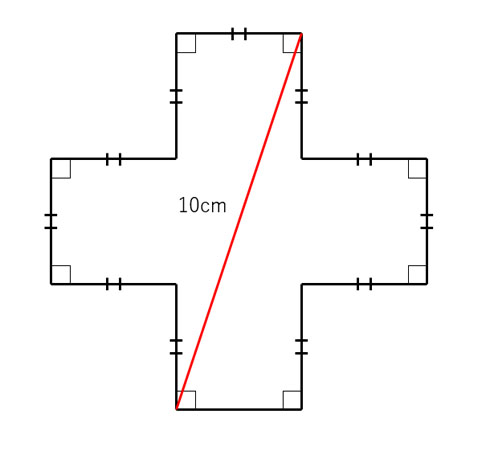
この図形の面積 三平方の定理を使わずに出せる ヒラメキで解く 算数 がちょっと手ごわい ねとらぼ

中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット

三平方の定理の利用 Ict教材eboard イーボード

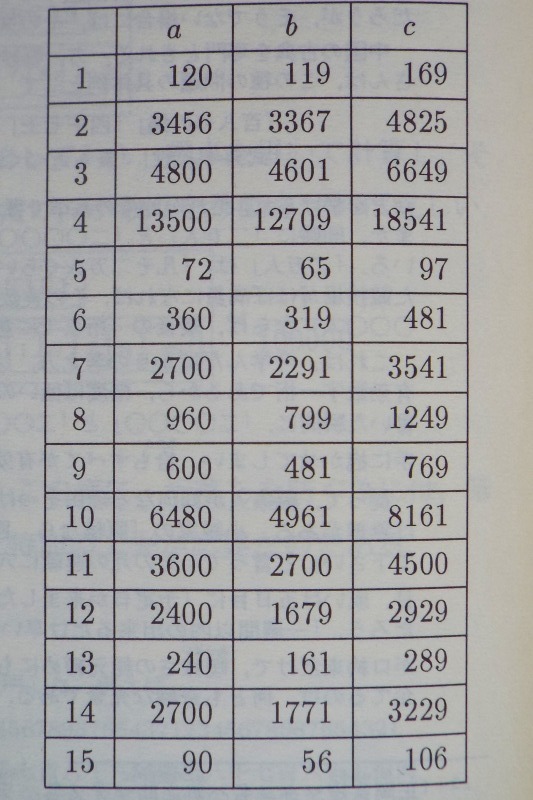
四千年前の三平方の定理 あざみ野夢工房

教えてください Clear

三平方の定理 覚えること 三角定規 苦手な数学を簡単に

三角比の表の値 Sincostan の覚え方を解説 単位円でマイナスも定義 遊ぶ数学

これで解決 タープ テントのロープの長さガイド 計算方法をわかりやすく解説 3ページ目 暮らし の

3分でわかる 三平方の定理 ピタゴラスの定理 の公式とは Qikeru 学びを楽しくわかりやすく

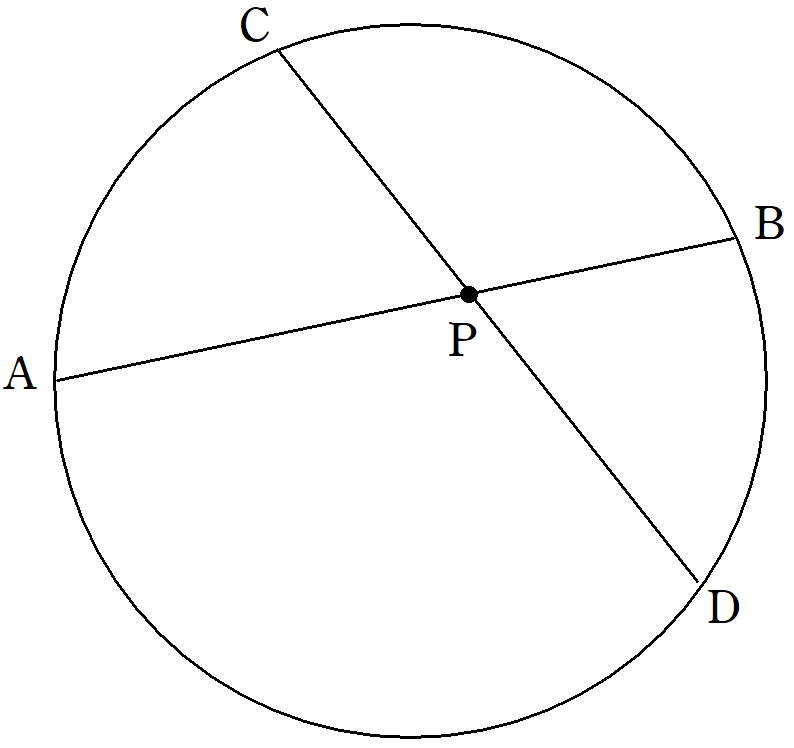
三平方の定理の証明 方べきの定理の利用１ Fukusukeの数学めも

三平方の定理 特別な直角三角形の3辺の比 中学生からの質問 数学 進研ゼミ中学講座 ベネッセコーポレーション

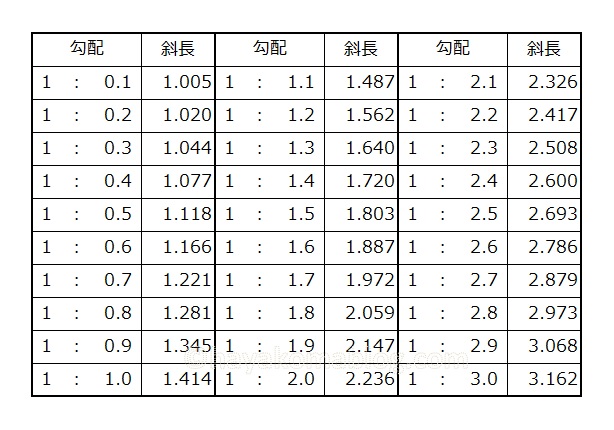
勾配 斜長 法長 斜辺 換算表

三平方の定理から四立方の定理へ 東京図書出版

三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者

単位円とは 1分でわかる意味 覚え方 表 Sin Tanとの関係

三平方の定理 自動計算サイト

三平方の定理

三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者

次の画像は芳賀の定理と呼ばれるもので 三平方の定理を証明するものに利用したり Yahoo 知恵袋

まとめるノート 中学数学

証明にこだわる

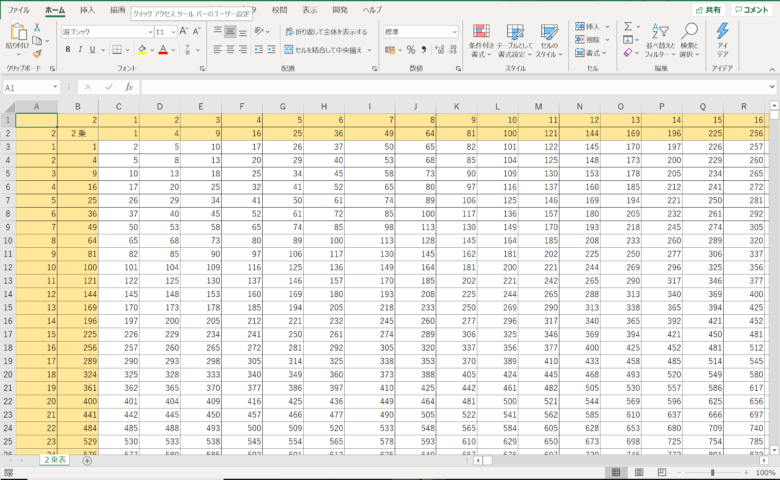
とピタゴラス数 Fukusukeの数学めも

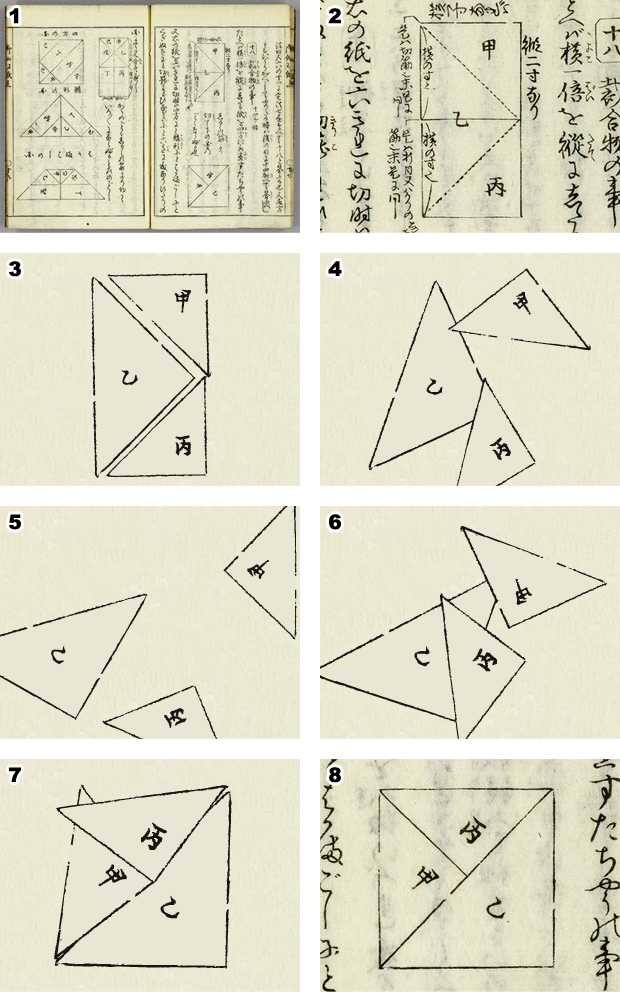
コラム ピタゴラスの定理 江戸の数学

三角比 高校物理の備忘録

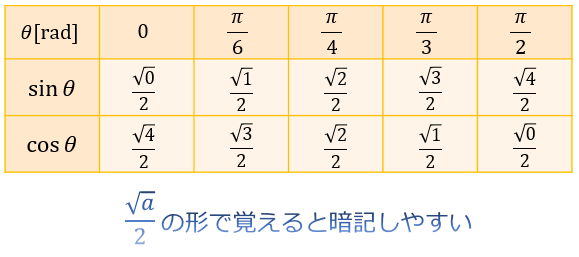
三角関数の基礎知識 Sin8 Cos8 Tan8 の覚え方 弧度法 三角比の表まとめ アタリマエ

中3 10 23 日 早朝 数学５時間特訓 三平方の定理 情熱特訓 ジーニアス 福島県須賀川市の学習進学塾

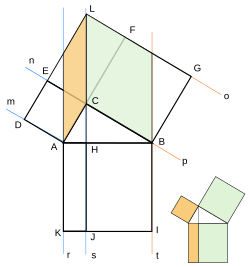
ピタゴラスの定理 Wikipedia

中学３年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生